Notas-funções
1 Teia de Notas-Funções
Essencialmente, tal modelo associa a cada acorde dentro de um campo tonal – ou, mais acuradamente, para cada categoria funcional possível – uma hierarquia para as notas estruturais de uma melodia que porventura harmonize. O ponto de partida para a construção desse modelo é o conceito conhecido pelos músicos como “escala de acordes”. Na perspectiva que nos é adequada, a escala de um acorde apresenta-se como uma maneira conveniente de dispor suas possibilidades de harmonização. A Figura 1 ilustra essa argumentação, considerando a escala referente ao acorde tônico (I) em Dó maior, cifrado, em sua versão tetrádica, como CM7.1

À esquerda da figura são apresentadas as notas-funções, dispostas em ordem escalar. As notas brancas correspondem às notas-estruturais básicas (identificadas abaixo da pauta), que formam o arpejo da tétrade – fundamental (1), terça (3), quinta (5) e a sétima maior (M7) –, incluindo a sexta (6), que eventualmente pode substituir a sétima.2 Para a avaliação das tensões elegíveis a integrar o grupo das notas-estruturais (acima da pauta) segue-se a regra prática dos “dois semitons”. Tal regra determina que uma nota-função não pertencente ao arpejo básico se candidataria a se tornar uma tensão harmonizável (portanto, uma nota-estrutural) para um acorde se, na escala, estiver a dois semitons acima da nota do arpejo imediatamente à sua esquerda. Em caso negativo (ou seja, se a distância for de apenas um semitom), a nota não é considerada para integrar o grupo das notas-estruturais, sendo denominada normalmente uma nota “evitada”.3
Uma representação verticalizada da escala, cuja principal vantagem é evidenciar a hierarquia das notas-estruturais, é apresentada à direita da Figura 1 (evidentemente, a nota “evitada” Fá é omitida). A partir desse conjunto de notas-estruturais estabelecido para o acorde CM7, funcionalmente contextualizado como I grau, podemos listar todas as possibilidades de concretização desse acorde, que são – importante acrescentar – equivalentes em relação à posição funcional: C (tríade), C.9 (tríade com nona acrescentada), CM7 (a disposição default, por assim dizer), C6, CM7.9 e C6.9 (ambas com a incorporação da tensão 9).
A partir dessa visão, propomos aqui uma acepção mais abrangente em relação à ideia tradicional de “harmonia”, a saber, como o conjunto resultante da combinação das notas formantes de um determinado acorde e das notas-estruturais presentes na melodia que ocorrem dentro desse contexto acordal. Frisamos que apenas as notas-estruturais são levadas em conta nesse somatório, desconsiderando-se assim toda e qualquer inflexão melódica que porventura ocorra nesse contexto. Definimos então, formalmente, uma inflexão como uma nota transitória que, podendo ou não pertencer à escala do acorde, é sucedida por uma nota claramente estrutural de si distanciada por grau conjunto, nota-estrutural esta denominada o alvo da inflexão. Inflexões, portanto, são elementos à parte do contexto acordal, não sendo registradas como estruturais.
Além da classificação de notas como estruturais ou inflexões, relacionadas a um contexto local (determinado pelos acordes que suportam as melodias), parece-nos também relevante avaliá-las de acordo com o contexto global (ou seja, a tonalidade a que pertencem), a partir de uma constatação de que melodias em música popular são predominantemente diatônicas e que notas não diatônicas são, em maior ou menor medida, digressões.
A partir desses conceitos, é possível propor uma metodologia de análise de melodias, considerando ambos os níveis – global e local. Como uma tentativa preliminar para formalizar um modelo analítico, a Figura 2 examina o exemplo de uma melodia hipotética.

Os dois níveis são contemplados na análise: abaixo da pauta são indicados os graus escalares associados a cada nota melódica através de números com circunflexos (contexto global), enquanto acima da pauta as notas-funções são evidenciadas, em relação aos acordes (contexto local). Inflexões são representadas pelo símbolo “\(\times\)”.
Observe-se que o método adotado promove normalização das melodias, ou seja, não é relevante a identificação das tonalidades absolutas envolvidas, apenas as relações entre as notas e as respectivas escalas diatônicas. Isso fica especialmente claro no exemplo através da modulação que acontece no compasso 4, com o contexto global transferindo-se de Lá maior para Fá maior (a troca de referencial escalar é representada pela fórmula “\(\hat{1} =\hat{3}\)”).
O modelo analítico contempla um processo algorítmico de análise das notas-funções, cuja entrada de dados é formatada como uma matriz de dimensões \(5 \times n\) (\(n\) é o número de notas da melodia, 36 no exemplo da Figura 2), denominada mapa de notas-funções (ou mapa NF). O quadro da Figura 3 apresenta o mapa NF referente aos três compassos iniciais da melodia da Figura 2.
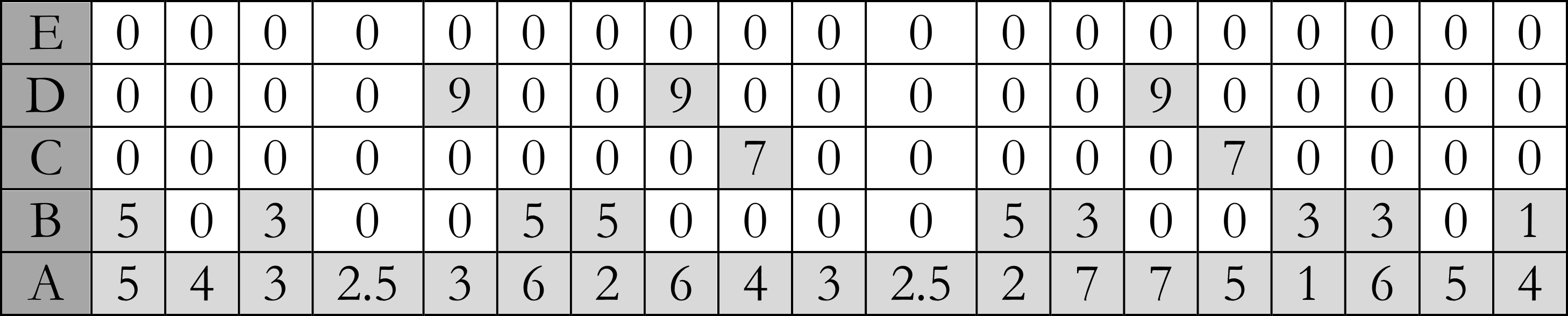
A coluna 1 do mapa identifica os níveis considerados:
- dos graus escalares (referente ao contexto global). Os números correspondentes aos graus são escritos sem os circunflexos originais. Alterações cromáticas são identificadas como números decimais (assim, 2.5 refere-se à alteração cromática ascendente do grau 2, ou seja, ao Si♯, no c. 1);4
- Notas-funções da tríade básica;
- Notas-funções da tétrade básica;
- Tensões simples;
- Tensões alteradas.
Com objetivos operacionais, facilitando a implementação computacional, um mapa a ser usado em análise é previamente preenchido por zeros. A cada coluna – cada nota – uma ou duas células são preenchidas: aquela referente à linha A (obrigatoriamente, pois o nível global precisa ser informado) e, se for o caso, uma das linhas de notas-estruturais (B-E). Se a nota em questão for uma inflexão, obviamente, apenas a célula da linha A será preenchida (para facilitar a visualização, as células preenchidas nos exemplos foram sombreadas).5
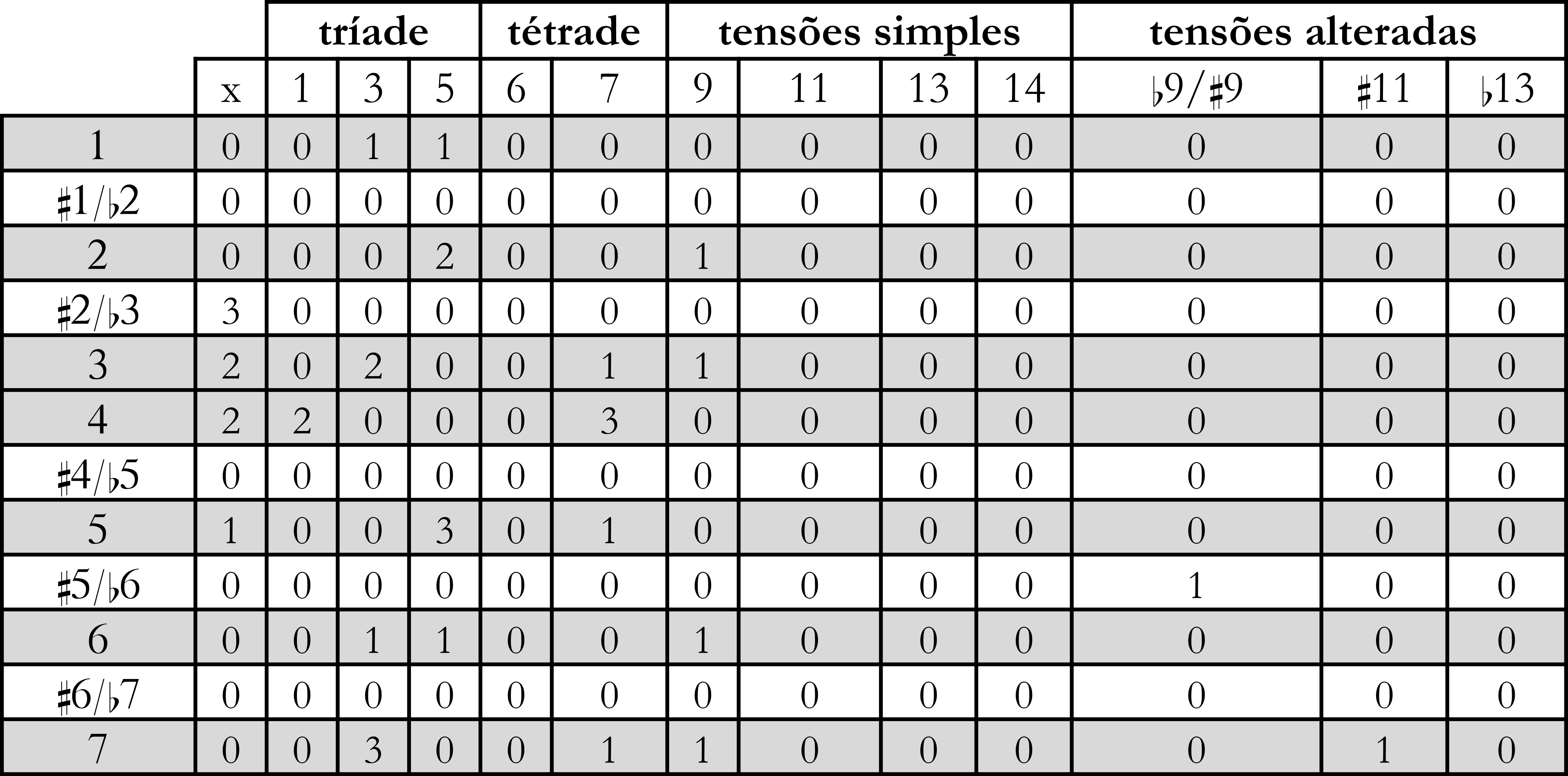
A computação da matriz NF pelo algoritmo de análise retorna uma matriz que dispõe as ocorrências de notas-funções em relação aos graus escalares, ou seja, combinando os contextos global e local. O quadro da Figura 4 apresenta a matriz-resultado referente ao exemplo da Figura 2.
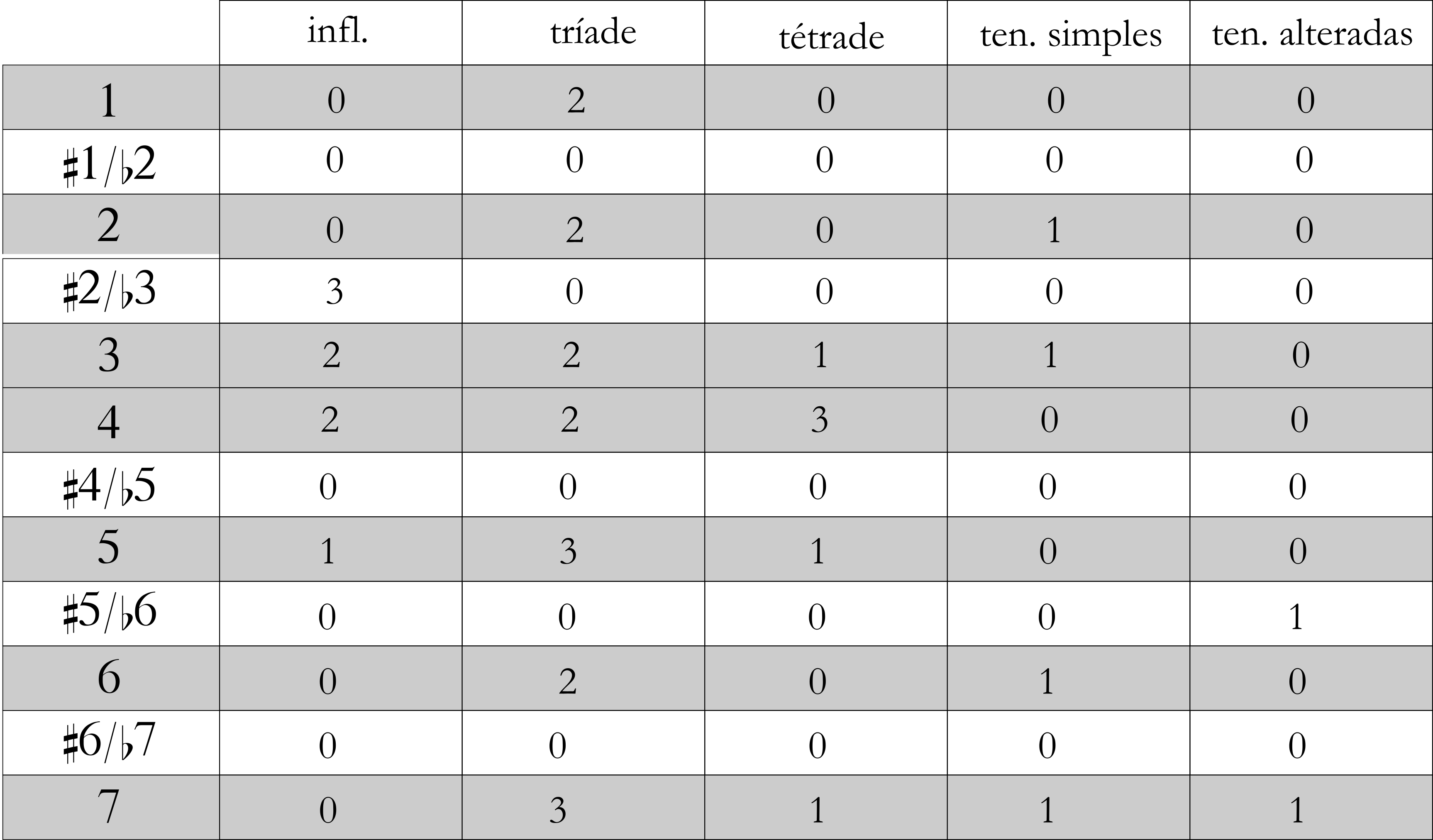
Uma versão mais concisa desse esquema considera apenas as cinco classes de notas-funções, ou seja, inflexões, notas-estruturais da tríade básica, notas-estruturais da tétrade, notas-estruturais correspondentes a tensões simples e notas-estruturais correspondentes a tensões alteradas (Figura 5). Assim, as categorias individuais colapsam nessas classes, o que facilita a plotagem gráfica (ver adiante) e proporciona um exame mais global da distribuição das notas-funções.
Uma das representações gráficas disponíveis no escopo do modelo é apresentada na Figura 6. Denominado Teia NF (a partir de seu formato, que lembra vagamente uma teia de aranha), o gráfico é formado por cinco círculos concêntricos cortados por 12 raios dispostos em incrementos angulares de 30°, com cada um desses eixos correspondendo a uma das notas da escala cromática. Os graus escalares (no caso da figura, considerando a escala diatônica maior) são identificados com algarismos arábicos (1 a 7), revelando sua superioridade hierárquica em relação aos graus escalares não diatônicos, os eixos intermediários.
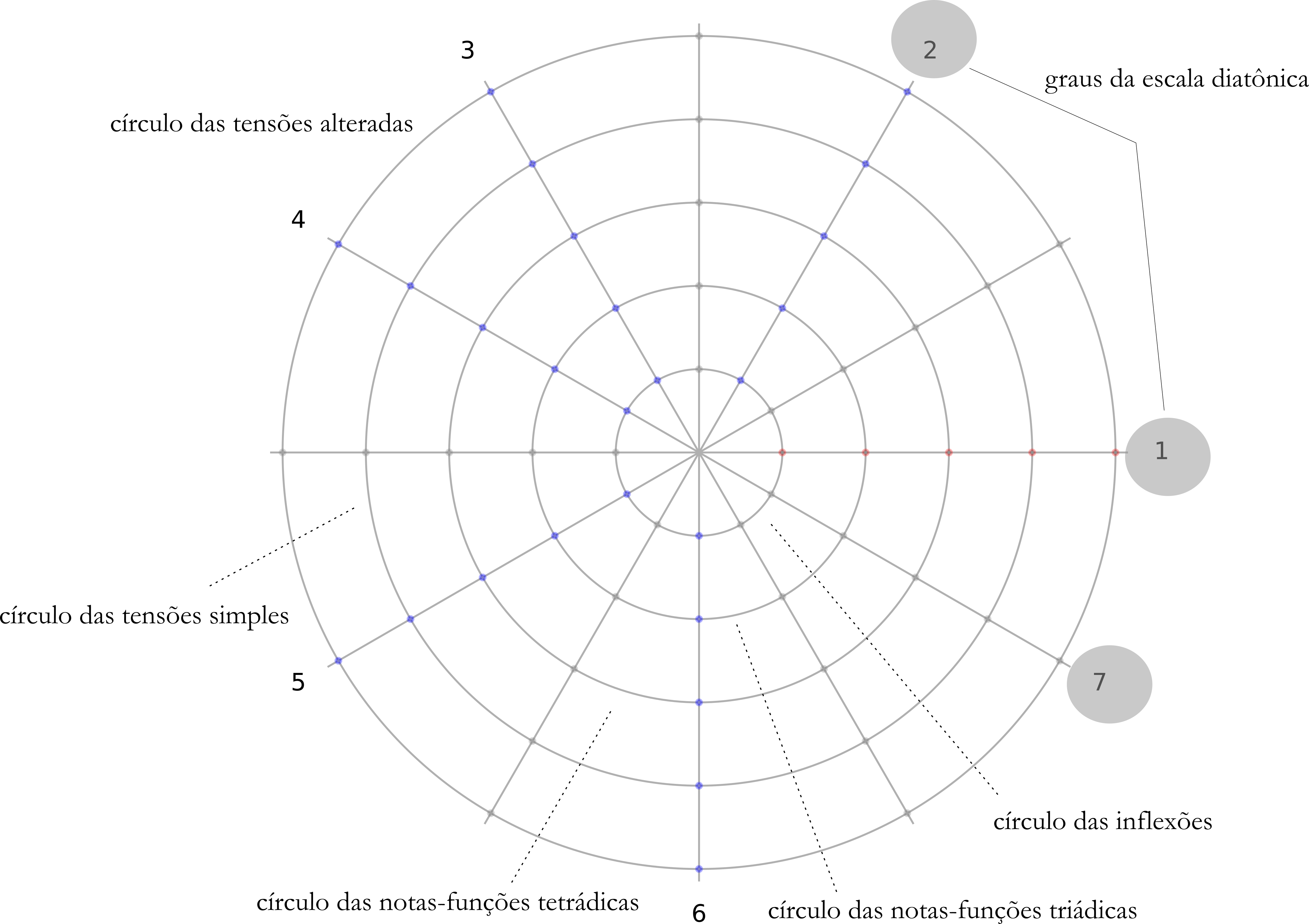
O círculo de menor raio corresponde ao nível das inflexões (órbita 1), com os demais círculos obedecendo a hierarquia das notas-estruturais, desde as mais básicas, que formam a tríade (órbita 2), passando pelas componentes da tétrade (órbita 3), as tensões simples (órbita 4) e, finalmente, as notas-estruturais mais fracamente “ancoradas”, as tensões alteradas, na órbita exterior (5).
A Teia NF tem, portanto, 60 posições possíveis, definidos pelos cruzamentos dos círculos e dos raios. De acordo com essa estrutura, é fácil concluir que melodias apoiadas em notas mais básicas tenderão a ter ocupadas na Teia correspondente mais posições “internas” do que “externas”. Por outro lado, melodias com relações mais complexas entre notas e acordes (como, por exemplo, em bossas novas), tenderão a “colonizar” posições mais “externas” das respectivas teias.
Uma métrica de grande importância para o modelo NF é o índice de ancoragem melódica (ia). Tal índice quantifica, em média, o comportamento de uma melodia em relação às notas-estruturais,6 tomando como parâmetro o grau de “ancoragem” dessas notas em relação aos acordes que as suportam. Entenda-se o termo como uma medida de maior ou menor proximidade de uma dada nota-estrutural em relação ao seu contexto acordal. Assim, quanto mais básica for a função exercida no acorde pela nota, mais “ancorada” ela estará.7
Referências
Notas de rodapé
As escalas dos sete acordes diatônicos recebem nomes associados com os chamados modos gregos: Jônica (I), Dórica (II), Frígia (III), Lídia (IV), Mixolídia (V), Eólia (VI) e Lócria (VII), cada qual com uma configuração intervalar distinta, o que se reflete nos respectivos conjuntos de notas-estruturais disponíveis.↩︎
Para uma explanação sobre notas-estruturais substitutas, ver Almada (2022).↩︎
Como em toda regra, há algumas exceções. Para sua apresentação e discussão, ver Almada (2022).↩︎
Observe que, como esse sistema não diferencia o sentido das alterações – bemóis e sustenidos –, a mesma designação (2.5) serviria para um cromatismo descendente do terceiro grau escalar (Dó natural, como acontece no c. 2 da Figura 2).↩︎
Em certo sentido, o mapa NF pode ser comparado com o espaço tonal de alturas (tonal pitch space) proposto por Lerdhal (2001), ambos configurados como estruturas estratificadas. As semelhanças, no entanto, são apenas essenciais, já que os dois esquemas são consideravelmente distintos em estrutura e em relação aos fenômenos que buscam mapear.↩︎
Ou seja, no cálculo do ia, apenas as notas-estruturais são levadas em conta, desconsiderando-se, assim, as inflexões presentes na melodia analisada.↩︎
Por uma questão de foco, postergamos, por ora, a apresentação cálculo do índice de ancoragem.↩︎
