Modelos teóricos

Este capítulo é dedicado a uma descrição sucinta dos modelos teóricos elaborados durante a pesquisa, considerando seus objetivos, escopos e conceitos.

1 Harmonia

A teoria associada ao domínio da harmonia dentro do projeto considera dois ramos principais – “semântico” e “sintático” –, nomeados numa relação metafórica com conceitos oriundos da Linguística. O ramo “semântico” dá conta especialmente das estruturas dos tipos acordais (ou TAs)¹ considerados, mas também de acordes específicos, enquanto o ramo “sintático” se refere às relações entre acordes e tipos acordais, considerando vários níveis de organização. As próximas subseções descrevem em linhas gerais dois modelos criados e desenvolvidos especialmente para a pesquisa: o dos Genera de Tipos Acordais (“semântico”) e o das Relações Binárias (“sintático”).

1.1 Genera de Tipos Acordais

O modelo teórico denominado Genera de Tipos Acordais (doravante identificado pelo acrônimo GTA) toma como base a existência de 10 tipos acordais arquetípicos, denominados protoacordes. De acordo com os pressupostos teóricos adotados, cada um destes tipos encabeça um conjunto (ou genus) de tipos acordais de mesma qualidade genérica, cujos membros são o próprio protoacorde e todas suas possíveis variantes. A derivação dos TAs, de acordo com o modelo, é regida por um conjunto de regras de produção e pela aplicação recursiva de três tipos de transformação: adição (inclusão de uma nota-função a um tipo acordal, como por exemplo, uma “nona” numa tríade maior), substituição (p. ex., a “terça” pela “quarta” no tipo acordal “dominante sus4”) e alteração (cromatização de uma nota-função referencial, resultando, p. ex., em uma “décima terceira” bemolizada). Os 10 genera são nomeados com letras finais do alfabeto em ordem inversa, maiúsculas referentes a protoacordes em modo maior, minúsculas para os protoacordes com terça menor.²

Protoacordes e variantes que integram um mesmo genus são identificados no sistema através de dois tipos de notação: (a) alfanumérica, baseada em uma simbologia aproximadamente consensual entre compositores e instrumentistas,³ e (b) genealógica, construída como uma fórmula que congrega o símbolo do genus e um código numérico que identifica a linhagem do TA em questão. Por convenção, todos os protoacordes são numerados com um “zero” à direita da letra-símbolo correspondente, como mostra a Tabela 1.

Tabela 1: Os 10 protoacordes do modelo GTA, considerando as notações genealógica e alfanumérica (com a fundamental “Dó” como referencial).

Genera	Notação genealógica	Notação alfanumérica
Z	Z0	CM7
Y	Y0	C7
X	X0	C(♭5)7
W	W0	C(♯5)7
V	V0	C
z	z0	Cm7
y	y0	Cø
x	x0	C°7
w	w0	Cm(M7)
v	v0	Cm

A aplicação das transformações sobre os protoacordes, condicionada pelas regras pré-estabelecidas (que incluem limites e restrições para evitar construções redundantes e “superpopulação” de TAs), permite a produção total de 161 variantes, distribuídas pelos genera em diferentes gerações (a geração “zero” corresponde ao nível dos protoacordes) como apresentado na Tabela 2.

Tabela 2: Distribuição dos TAs pelos 10 genera.

Genera	0	1	2	3	4	5	6	Total
Z	1	5	7	3	-	-	-	16
Y	1	4	9	14	16	13	2	59
X	1	3	5	6	4	-	-	19
W	1	2	3	3	1	-	-	10
V	1	4	5	2	-	-	-	12
z	1	3	4	3	-	-	-	11
y	1	3	3	1	-	-	-	8
x	1	4	6	3	1	-	-	15
w	1	2	1	-	-	-	-	4
v	1	3	3	1	-	-	-	8
Total	10	33	46	36	22	13	2	161

Como se observa nessa distribuição, enquanto alguns genera são bastante rarefeitos (como v, com apenas oito membros) outros apresentam alta densidade, notavelmente o genus “dominante” Y, com 59 elementos, o que se explica especialmente pela disponibilidade e possibilidades combinatórias decorrentes de um rico cardápio de tensões (e de suas possíveis alterações).

A notação genealógica de variantes descreve sua posição derivativa dentro do genus respectivo através de uma sequência numérica. Por exemplo, o rótulo Y1321 representa o TA variante do genus Y de quarta geração (o que se depreende pelo número de algarismos que se seguem à letra identificadora). Sua posição genealógica (lida da direita para a esquerda) é: primeira variante (4ª geração) da segunda variante (3ª geração) da terceira variante (2ª geração) da primeira variante (1ª geração) de Y0.

1.2 Relações Binárias

O segundo modelo corresponde à Teoria das Relações Binárias (TRB), sendo destinado à quantificação e qualificação dos encadeamentos entre pares de “atores harmônicos” contíguos. Entenda-se este termo como uma designação genérica que pode representar diversos níveis de informação harmônica. Assim, o modelo comporta não apenas tipos acordais (como foi concebido originalmente), mas também acordes específicos, categorias funcionais e mesmo relações tonais. Os quatro níveis de relações binárias considerados são os seguintes:

1. Relações binárias acordais específicas (RBs) – é o nível mais baixo, correspondendo à descrição da relação entre dois TAs específicos contíguos. Devido ao gigantesco número de possibilidades,⁴ esse tipo não é contabilizado nas análises, embora seja importante seu registro, pois cria a base sobre a qual os demais níveis se apresentam. As relações binárias (por simplicidade, RBs) podem ser denotadas tanto em notação convencional por cifras alfanuméricas – por exemplo, C7.9.13 | Am6.9 – quanto em notação genealógica, de acordo com o modelo GTA. Neste caso, é adotada a fórmula \[Q_1|i Q_2,\] onde \(Q_1\) e \(Q_2\) são os símbolos genealógicos referentes aos TAs que formam a relação e \(i\) é o intervalo entre suas fundamentais, em módulo 12 (\(0 \leq i \leq 11\)). Assim, o exemplo acima apresentado da RB em cifras (C7.9.13 | Am6.9), é notado genealogicamente como Y22|9z11, de acordo com a classificação lexical dos TAs.

2. Relações binárias acordais abstratas (RBAs) – este nível filtra do anterior apenas as informações essenciais da relação binária acordal, ou seja, o intervalo entre as fundamentais dos dois tipos acordais contíguos e seus respectivos genera, daí a designação “abstrata”. Posto de outra maneira, uma RBA retira de uma relação binária acordal específica as identificações das variantes dos TAs envolvidos. Considerando o exemplo anterior, sua notação como RBA passa a ser Y|9z. Essa filtragem permite que o número de alternativas seja drasticamente reduzido, tornando as RBAs adequadas para mapeamentos e manipulações estatísticas.

3. Relações binárias funcionais (RBFs) – neste caso, os aspectos harmônicos considerados da relação binária são as categorias funcionais associadas aos tipos acordais. Em outros termos, o tipo identifica o contexto em que se dá a relação, considerando um nível “sintático” mais alto do que o das RBs e RBAs. Há 73 categorias funcionais (codificadas numericamente) mapeadas no sistema, agrupadas em 11 classes.⁵ Uma RBF é notada de acordo com a fórmula \[F_1|F_2,\] onde \(F_1\) e \(F_2\) são os símbolos funcionais referentes aos TAs que formam a relação. Por exemplo: V|I, SubV/IV|IV etc.

4. Relações binárias tonais (RBTs) – informam as relações de mais alto nível, ou seja, aquelas que envolvem tonalidades contíguas em uma única peça musical em análise. Considerando que há 12 tônicas (as 12 classes de altura) e dois modos (maior e menor), o número de combinações possíveis é 48. Adotamos para designação das RBTs uma fórmula adaptada daquela proposta por Murphy (2006) : \[T_1iT_2,\] onde \(T_1\) e \(T_2\) são os símbolos que representam os modos das tonalidades formam a relação (“M” é usado para modo maior e “m” para modo menor) e \(i\) é o intervalo entre suas tônicas, em módulo 12 (\(0 \leq i \leq 11\)). Por exemplo: M7m, m0M etc. As RBTs são agrupadas em classes:

   • RBTs notáveis – congregam as modulações mais comuns. Suas subclasses são:
     • REL (relativas) – entre tonalidades relativas: M9m e m3M;
     • D/SD (dominantes/subdominantes) – entre tonalidades de mesmo modo distanciadas por quartas justas: M5M, M7M, m5m e m7m;
     • HOM (homônimas) – entre tonalidades de modos distintos e mesma tônica: m0M e M0m.
   • Demais RBTs – cujas subclasses são:
     • Mediânticas (MED) – entre tonalidades distanciadas por terça:⁶ M3M, M4M, M8M, M9M, M3m, M4m, M8m, m4M, m8M, m9M, m3m, m4m, m8m e m9m;
     • Quartais (QUA) – entre tonalidades distanciadas por quarta justa:⁷ M5m, M7m, m5M e m7M;
     • Contíguas por semitom (STM) – entre tonalidades distanciadas por um semitom: M1M, M11M, M1m, M11m, m1M, m11M, m1m e m11m;
     • Contíguas por tom (TOM) – entre tonalidades distanciadas por um tom: M2M, M10M, M2m, M10m, m2M, m10M, m2m e m10m;
     • Tritônicas (TRI) – entre tonalidades distanciadas por trítono: M6M, M6m, m6M e m6m.

2 Melodia

2.1 Filtragem Melódica

As bases para a construção deste modelo foram definidas a partir de três princípios: segmentação, abstração e codificação. O primeiro deles se fundamenta na ideia de que o entendimento de uma informação sequencial requer que esta seja segmentada em unidades de menor extensão cada qual exercendo uma relativa autonomia (como pequenas “frases” musicais ou, de uma maneira mais neutra, como pequenos grupos).⁸ No modelo, tais grupos são denominados palavras.⁹ Já a abstração é um estágio imprescindível para qualquer processo analítico, pois permite que estruturas distintas possam ser agrupadas em classes de equivalência em relação a algum parâmetro de comparação. No modelo de Filtragem Melódica (abreviado como FM), as estruturas de alturas e rítmica são isoladas das melodias em análise, transformando-se em descrições abstratas desses domínios. Desse modo, as alturas são transcritas como sequências de sete gestos básicos de contorno (repetições de nota, graus conjuntos, arpejos e saltos, ascendentes e descendentes) – formando um alfabeto de c-letras (Figura 1).

Figura 1: Alfabeto de c-letras.

Para o ritmo, a estratégia consiste em subdividir um tempo (semínima) em 12 unidades e associar as possíveis configurações de IOIs¹⁰ que ocorrem dentro dessa janela temporal a unidades-padrão, denominadas no modelo r-letras, o que permite a formação de um alfabeto com 26 elementos (Figura 2).

Figura 2: Alfabeto de r-letras.

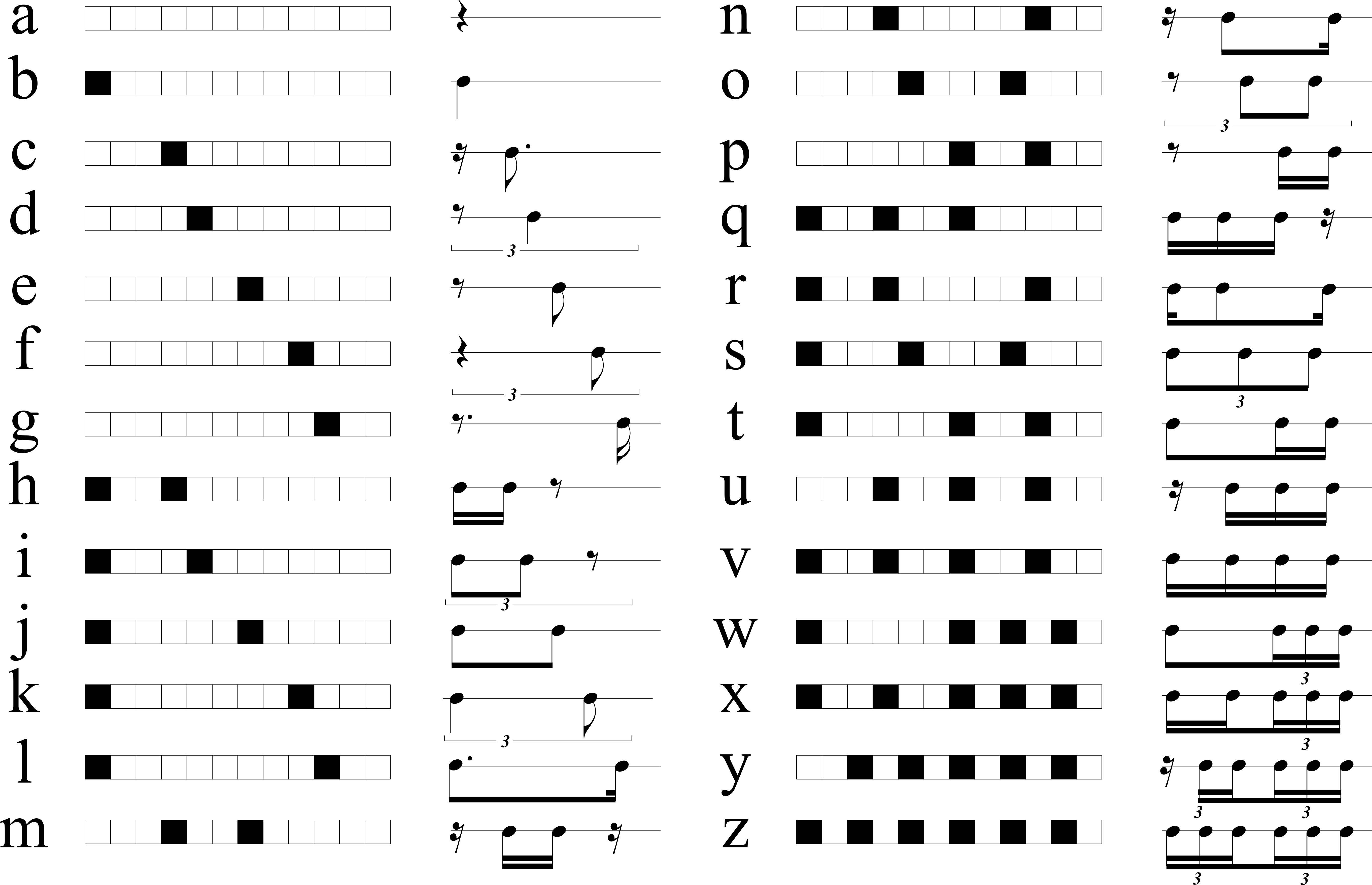
Finalmente, a codificação associa as c- e r-letras a símbolos alfabéticos, que passam a ser usados na tradução computacional das estruturas de alturas e rítmicas, transformando melodias em sequências segmentadas de c-palavras e r-palavras (Figura 3).

Figura 3: Exemplo de uma c/r-palavra.

Recentemente, um novo conceito foi incorporado ao modelo, o de r-sílabas.¹¹ Tratam-se de unidades rítmicas de nível intermediário em relação às r-letras e r-palavras, que trazem pontencialmente ao entendimento do ritmo uma carga “semântica”, já que podem ser associadas a pequenos motivos rítmicos. Embora r-sílabas possam em tese apresentar diferentes cardinalidades, consideramos como as categorias ótimas para análise os r-dissílabos (r-sílaba com duas r-letras, por exemplo, nc) e os r-trissílabos, (jjl, por exemplo). Cada um dos níveis (letra, sílaba e palavra) será base para alguns atributos estilísticos, como será apresentado oportunamente.

2.2 Teia de Notas-Funções

Essencialmente, tal modelo associa a cada acorde dentro de um campo tonal – ou, mais acuradamente, para cada categoria funcional possível – uma hierarquia para as notas estruturais de uma melodia que porventura harmonize. O ponto de partida para a construção desse modelo é o conceito conhecido pelos músicos como “escala de acordes”. Na perspectiva que nos é adequada, a escala de um acorde apresenta-se como uma maneira conveniente de dispor suas possibilidades de harmonização. A Figura 4 ilustra essa argumentação, considerando a escala referente ao acorde tônico (I) em Dó maior, cifrado, em sua versão tetrádica, como CM7.¹²

Figura 4: Estrutura da escala de CM7 (I em Dó maior) e identificação de suas notas-estruturais.

À esquerda da figura são apresentadas as notas-funções, dispostas em ordem escalar. As notas brancas correspondem às notas-estruturais básicas (identificadas abaixo da pauta), que formam o arpejo da tétrade – fundamental (1), terça (3), quinta (5) e a sétima maior (M7) –, incluindo a sexta (6), que eventualmente pode substituir a sétima.¹³ Para a avaliação das tensões elegíveis a integrar o grupo das notas-estruturais (acima da pauta) segue-se a regra prática dos “dois semitons”. Tal regra determina que uma nota-função não pertencente ao arpejo básico se candidataria a se tornar uma tensão harmonizável (portanto, uma nota-estrutural) para um acorde se, na escala, estiver a dois semitons acima da nota do arpejo imediatamente à sua esquerda. Em caso negativo (ou seja, se a distância for de apenas um semitom), a nota não é considerada para integrar o grupo das notas-estruturais, sendo denominada normalmente uma nota “evitada”.¹⁴

Uma representação verticalizada da escala, cuja principal vantagem é evidenciar a hierarquia das notas-estruturais, é apresentada à direita da Figura 4 (evidentemente, a nota “evitada” Fá é omitida). A partir desse conjunto de notas-estruturais estabelecido para o acorde CM7, funcionalmente contextualizado como I grau, podemos listar todas as possibilidades de concretização desse acorde, que são – importante acrescentar – equivalentes em relação à posição funcional: C (tríade), C.9 (tríade com nona acrescentada), CM7 (a disposição default, por assim dizer), C6, CM7.9 e C6.9 (ambas com a incorporação da tensão 9).

A partir dessa visão, propomos aqui uma acepção mais abrangente em relação à ideia tradicional de “harmonia”, a saber, como o conjunto resultante da combinação das notas formantes de um determinado acorde e das notas-estruturais presentes na melodia que ocorrem dentro desse contexto acordal. Frisamos que apenas as notas-estruturais são levadas em conta nesse somatório, desconsiderando-se assim toda e qualquer inflexão melódica que porventura ocorra nesse contexto. Definimos então, formalmente, uma inflexão como uma nota transitória que, podendo ou não pertencer à escala do acorde, é sucedida por uma nota claramente estrutural de si distanciada por grau conjunto, nota-estrutural esta denominada o alvo da inflexão. Inflexões, portanto, são elementos à parte do contexto acordal, não sendo registradas como estruturais.

Além da classificação de notas como estruturais ou inflexões, relacionadas a um contexto local (determinado pelos acordes que suportam as melodias), parece-nos também relevante avaliá-las de acordo com o contexto global (ou seja, a tonalidade a que pertencem), a partir de uma constatação de que melodias em música popular são predominantemente diatônicas e que notas não diatônicas são, em maior ou menor medida, digressões.

A partir desses conceitos, é possível propor uma metodologia de análise de melodias, considerando ambos os níveis – global e local. Como uma tentativa preliminar para formalizar um modelo analítico, a Figura 5 examina o exemplo de uma melodia hipotética.

Figura 5: Exemplo de análise melódica (considerando contextos local e global) de uma melodia hipotética.

Os dois níveis são contemplados na análise: abaixo da pauta são indicados os graus escalares associados a cada nota melódica através de números com circunflexos (contexto global), enquanto acima da pauta as notas-funções são evidenciadas, em relação aos acordes (contexto local). Inflexões são representadas pelo símbolo “\(\times\)”.

Observe-se que o método adotado promove normalização das melodias, ou seja, não é relevante a identificação das tonalidades absolutas envolvidas, apenas as relações entre as notas e as respectivas escalas diatônicas. Isso fica especialmente claro no exemplo através da modulação que acontece no compasso 4, com o contexto global transferindo-se de Lá maior para Fá maior (a troca de referencial escalar é representada pela fórmula “\(\hat{1} =\hat{3}\)”).

O modelo analítico contempla um processo algorítmico de análise das notas-funções, cuja entrada de dados é formatada como uma matriz de dimensões \(5 \times n\) (\(n\) é o número de notas da melodia, 36 no exemplo da Figura 5), denominada mapa de notas-funções (ou mapa NF). O quadro da Figura 6 apresenta o mapa NF referente aos três compassos iniciais da melodia da Figura 5.

Figura 6: Mapa de notas-funções referente ao exemplo da Figura 5, c. 1-3.

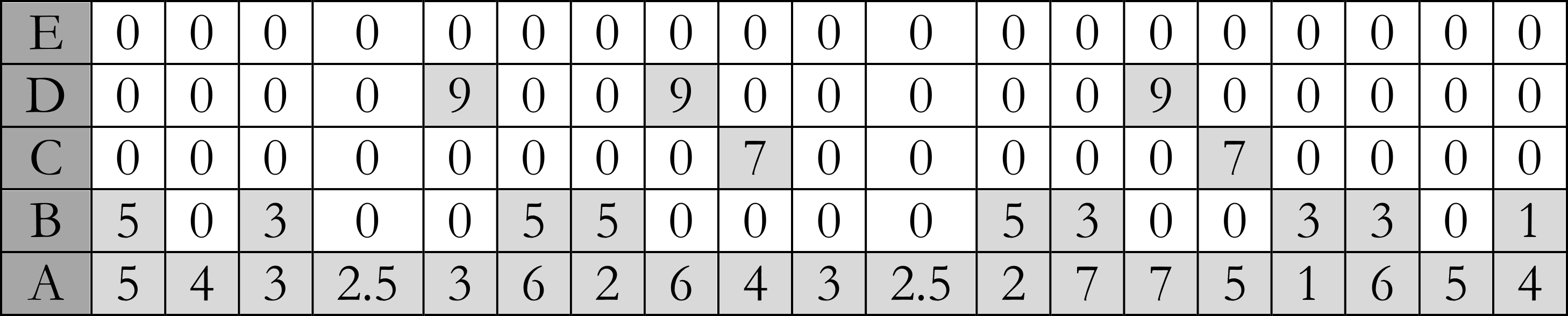
A coluna 1 do mapa identifica os níveis considerados:

1. dos graus escalares (referente ao contexto global). Os números correspondentes aos graus são escritos sem os circunflexos originais. Alterações cromáticas são identificadas como números decimais (assim, 2.5 refere-se à alteração cromática ascendente do grau 2, ou seja, ao Si♯, no c. 1);¹⁵
2. Notas-funções da tríade básica;
3. Notas-funções da tétrade básica;
4. Tensões simples;
5. Tensões alteradas.

Com objetivos operacionais, facilitando a implementação computacional, um mapa a ser usado em análise é previamente preenchido por zeros. A cada coluna – cada nota – uma ou duas células são preenchidas: aquela referente à linha A (obrigatoriamente, pois o nível global precisa ser informado) e, se for o caso, uma das linhas de notas-estruturais (B-E). Se a nota em questão for uma inflexão, obviamente, apenas a célula da linha A será preenchida (para facilitar a visualização, as células preenchidas nos exemplos foram sombreadas).¹⁶

A computação da matriz NF pelo algoritmo de análise retorna uma matriz que dispõe as ocorrências de notas-funções em relação aos graus escalares, ou seja, combinando os contextos global e local. O quadro da Figura 7 apresenta a matriz-resultado referente ao exemplo da Figura 5.

Figura 7: Matriz de notas-funções referente ao exemplo da Figura 5.

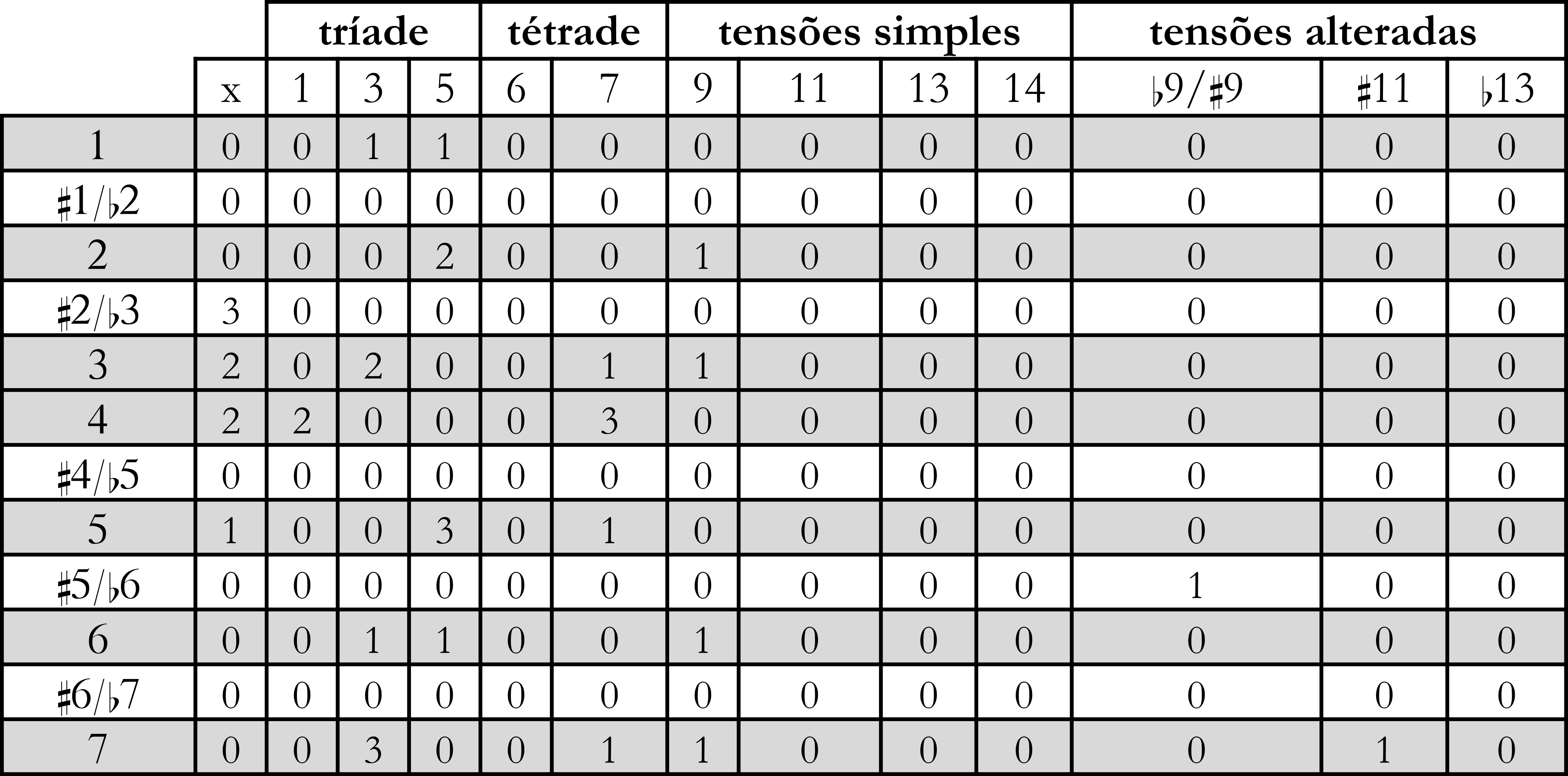
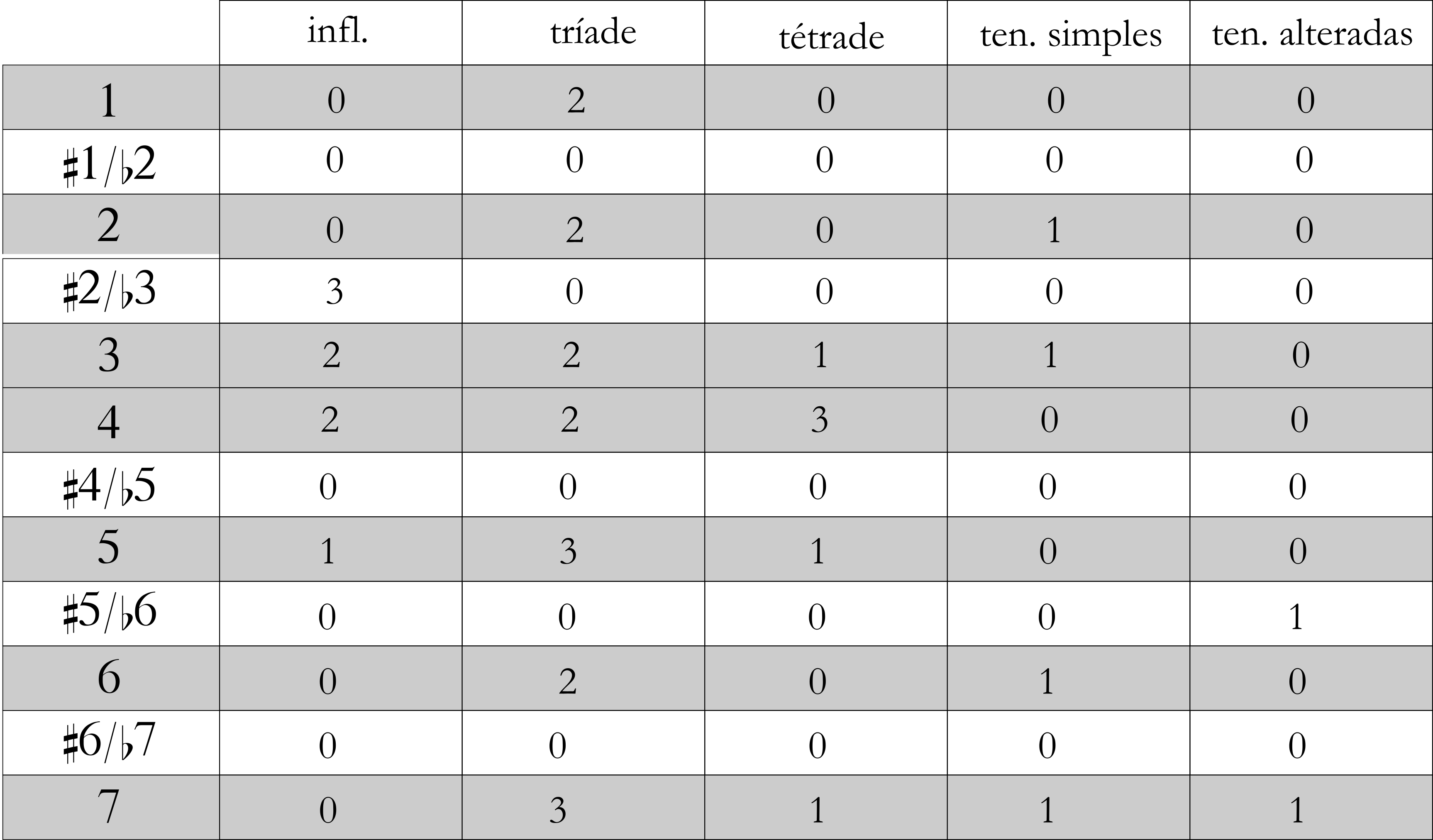
Uma versão mais concisa desse esquema considera apenas as cinco classes de notas-funções, ou seja, inflexões, notas-estruturais da tríade básica, notas-estruturais da tétrade, notas-estruturais correspondentes a tensões simples e notas-estruturais correspondentes a tensões alteradas (Figura 8). Assim, as categorias individuais colapsam nessas classes, o que facilita a plotagem gráfica (ver adiante) e proporciona um exame mais global da distribuição das notas-funções.

Figura 8: Matriz de classes de notas-funções referente ao exemplo da Figura 5.

Uma das representações gráficas disponíveis no escopo do modelo é apresentada na Figura 9. Denominado Teia NF (a partir de seu formato, que lembra vagamente uma teia de aranha), o gráfico é formado por cinco círculos concêntricos cortados por 12 raios dispostos em incrementos angulares de 30°, com cada um desses eixos correspondendo a uma das notas da escala cromática. Os graus escalares (no caso da figura, considerando a escala diatônica maior) são identificados com algarismos arábicos (1 a 7), revelando sua superioridade hierárquica em relação aos graus escalares não diatônicos, os eixos intermediários.

Figura 9: Esquema básico da Teia NF.

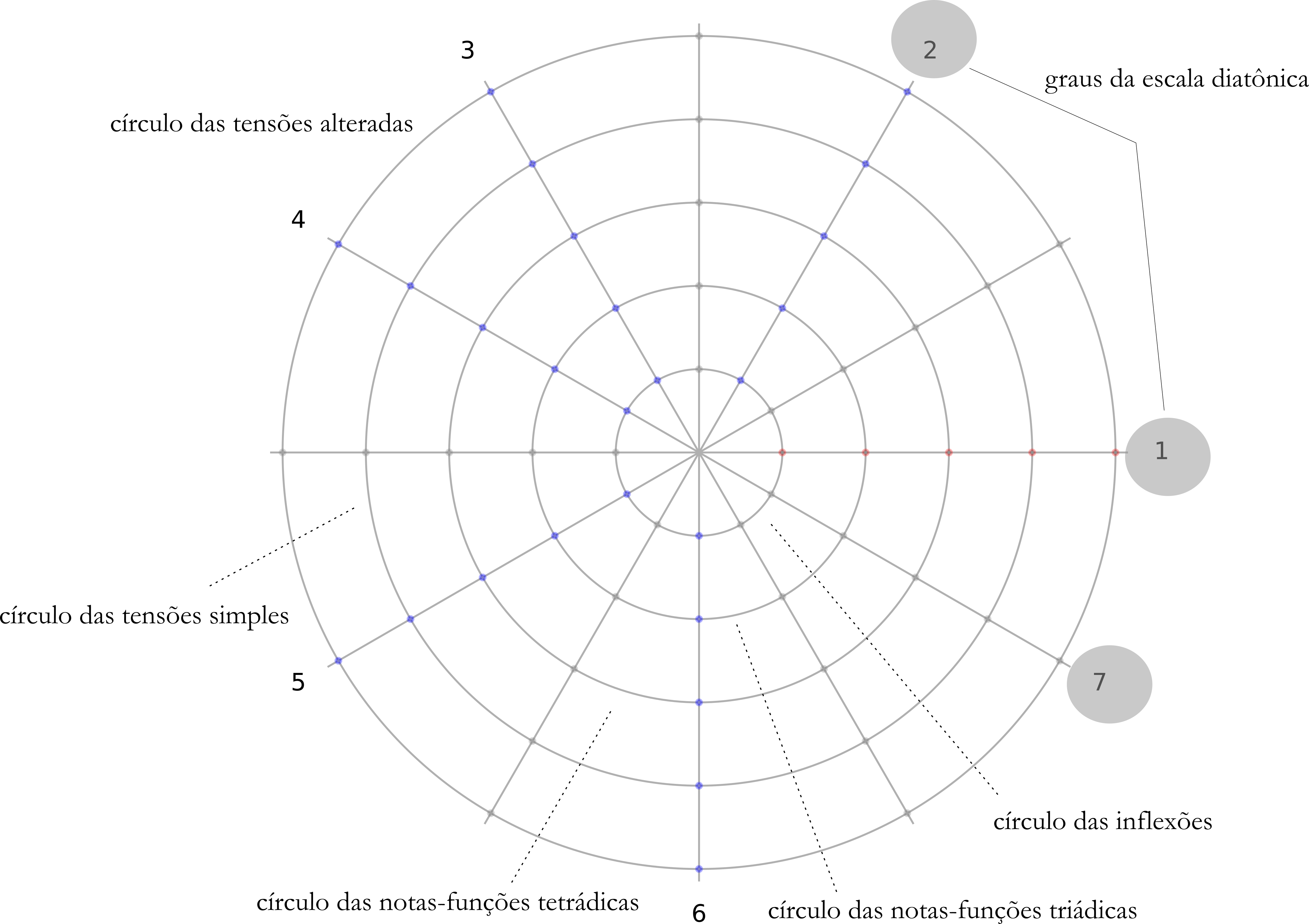
O círculo de menor raio corresponde ao nível das inflexões (órbita 1), com os demais círculos obedecendo a hierarquia das notas-estruturais, desde as mais básicas, que formam a tríade (órbita 2), passando pelas componentes da tétrade (órbita 3), as tensões simples (órbita 4) e, finalmente, as notas-estruturais mais fracamente “ancoradas”, as tensões alteradas, na órbita exterior (5).

A Teia NF tem, portanto, 60 posições possíveis, definidos pelos cruzamentos dos círculos e dos raios. De acordo com essa estrutura, é fácil concluir que melodias apoiadas em notas mais básicas tenderão a ter ocupadas na Teia correspondente mais posições “internas” do que “externas”. Por outro lado, melodias com relações mais complexas entre notas e acordes (como, por exemplo, em bossas novas), tenderão a “colonizar” posições mais “externas” das respectivas teias.

Uma métrica de grande importância para o modelo NF é o índice de ancoragem melódica (ia). Tal índice quantifica, em média, o comportamento de uma melodia em relação às notas-estruturais,¹⁷ tomando como parâmetro o grau de “ancoragem” dessas notas em relação aos acordes que as suportam. Entenda-se o termo como uma medida de maior ou menor proximidade de uma dada nota-estrutural em relação ao seu contexto acordal. Assim, quanto mais básica for a função exercida no acorde pela nota, mais “ancorada” ela estará.¹⁸

Referências

Almada, Carlos. 2022. A Harmonia de Jobim. Campinas: Editora da Unicamp.

Almada, Carlos, e Pedro Zisels. 2023. «O ritmo de ideias básicas de samba: uma abordagem sistemática». Musica Theorica 8 (1).

Lerdhal, Fred. 2001. Tonal Pitch Space. Oxford: Oxford University Press.

Murphy, Scott. 2006. «The Major Tritone Progression in Recent Hollywood Science Fiction Films». Music Theory Online 12 (2).

Snyder, Robert. 2001. Music and Memory: An Introduction. Cambridge: The MIT Press.

Notas de rodapé

1. Entende-se este conceito como uma versão abstrata da ideia de um acorde, na qual sua fundamental específica passa a ser irrelevante. Num tipo acordal (doravante, TA) é filtrada a qualidade do acorde, manifestada principalmente pela estrutura intervalar entre seus componentes. Assim, por exemplo, a qualidade “dominante-com-nona-maior” de um acorde específico A7.9 é, em suma, seu tipo acordal associado, consistindo na sequência intervalar <2233> (em número de semitons), resultante da disposição compactada das classes de alturas <A-B-C♯-E-G>.

2. Para uma descrição mais detalhada do modelo GTA, ver Almada (2022).

3. Os modelos adotam um sistema de cifragem próprio, cuja principal distinção se refere ao ordenamento dos símbolos numéricos eventualmente empregados no rótulo e o uso de pontos de separação dos símbolos (além de parênteses, nos casos em que há alteração de notas-funções). Por exemplo: C6.M7.9, E4.7(♭9)13, F(♯5)7 etc. Para maiores detalhes sobre o sistema de notação alfanumérica, ver Almada (2022).

4. Considerando a estrutura teórica que fundamenta a pesquisa, o total possível de RBs é 311.052 (161 \(\times\) 12 \(\times\) 12).

5. A listagem das categorias e classes funcionais será apresentada em um capítulo específico.

6. Excluindo-se aqui, evidentemente, as relativas (REL) M9m e m3M, já contabilizadas entre as relações notáveis.

7. Excluindo-se aqui, evidentemente, as modulações dominante/subdominante (D/SD) M5M, M7M, m5m e m7m, já contabilizadas entre as relações notáveis.

8. Para um suporte a essa argumentação, ver Snyder (2001).

9. O que denota mais uma correlação metafórica com conceitos linguísticos.

10. Na sigla em inglês, Inter-Onset Intervals (intervalos entre ataques). Em sequências de IOIs, as durações não são levadas em conta, apenas as distâncias entre pontos de ataque.

11. Almada e Zisels (2023)

12. As escalas dos sete acordes diatônicos recebem nomes associados com os chamados modos gregos: Jônica (I), Dórica (II), Frígia (III), Lídia (IV), Mixolídia (V), Eólia (VI) e Lócria (VII), cada qual com uma configuração intervalar distinta, o que se reflete nos respectivos conjuntos de notas-estruturais disponíveis.

13. Para uma explanação sobre notas-estruturais substitutas, ver Almada (2022).

14. Como em toda regra, há algumas exceções. Para sua apresentação e discussão, ver Almada (2022).

15. Observe que, como esse sistema não diferencia o sentido das alterações – bemóis e sustenidos –, a mesma designação (2.5) serviria para um cromatismo descendente do terceiro grau escalar (Dó natural, como acontece no c. 2 da Figura 5).

16. Em certo sentido, o mapa NF pode ser comparado com o espaço tonal de alturas (tonal pitch space) proposto por Lerdhal (2001), ambos configurados como estruturas estratificadas. As semelhanças, no entanto, são apenas essenciais, já que os dois esquemas são consideravelmente distintos em estrutura e em relação aos fenômenos que buscam mapear.

17. Ou seja, no cálculo do ia, apenas as notas-estruturais são levadas em conta, desconsiderando-se, assim, as inflexões presentes na melodia analisada.

18. Por uma questão de foco, postergamos, por ora, a apresentação cálculo do índice de ancoragem.